Shamir's Secret Sharing: Polynomial Interpolation Over GF(256)

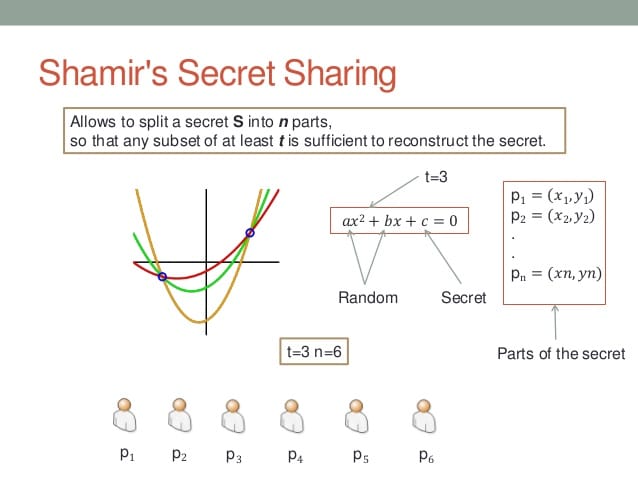
The system works by encoding your secret as the constant term (a₀) of a polynomial. If you want a 3-of-5 scheme (any 3 shares out of 5 total can reconstruct the secret), you create a degree-2 polynomial: f(x) = a₀ + a₁x + a₂x². The secret becomes a₀, while a₁ and a₂ are random numbers chosen from cryptographically secure sources.

You generate shares by evaluating this polynomial at different x-values. Share 1 gets f(1), share 2 gets f(2), and so on. Each share is the coordinate pair (x, f(x)). Never use x=0 because f(0) = a₀ = your secret, immediately exposing everything to whoever holds that share.

Reconstruction uses Lagrange interpolation. With any k shares from a degree k-1 polynomial, you can calculate the original polynomial and extract a₀. This mathematical property guarantees that k-1 shares provide zero information about the secret, regardless of computational power available to attackers.

Finite Field Implementation

Shamir's scheme works over any finite field GF(q), not specifically GF(256). Most implementations use GF(256) because it maps to bytes, making computer implementation efficient. GF(256) performs arithmetic modulo an irreducible polynomial of degree 8, typically x⁸ + x⁴ + x³ + x + 1.

In GF(256), addition equals XOR operations. Multiplication requires more complex field arithmetic, often implemented through logarithm tables that convert multiplication to addition. However, standard table lookups create timing side-channels through cache behavior. Constant-time implementations require specialized techniques like bit-slicing or scanning entire tables, sacrificing speed for security.

The choice of irreducible polynomial affects implementation performance but not security properties. All degree-8 irreducible polynomials create mathematically equivalent (isomorphic) fields, so security remains identical regardless of which one you select.

Critical Security Requirements

Random coefficient generation demands uniform distribution over the chosen finite field. Weak randomness breaks information-theoretic security guarantees by enabling statistical analysis of coefficients. The mathematical requirement is uniform, cryptographically secure randomness - compliance terms like "approved generators" reflect policy, not mathematical necessity.

Standard Shamir's Secret Sharing cannot verify share authenticity or detect corruption. Polynomial reconstruction with corrupted shares produces garbage output without warning. Verifiable Secret Sharing schemes like Feldman or Pedersen commitments add cryptographic proofs that enable share validation, but require additional computational overhead and assumptions.

Memory management becomes critical during implementation. Secrets, shares, and intermediate computation values must be explicitly cleared from memory to prevent recovery through cold boot attacks, memory dumps, or swap file analysis. Standard memory allocation provides no protection against these attack vectors.

Implementation Realities

Finite field arithmetic operates under exact modular mathematics - there's no "numerical stability" or "overflow" in the floating-point sense. Computational correctness and side-channel resistance represent the primary implementation challenges, not mathematical precision issues.

Lagrange interpolation scales as O(k²) for k shares using naive algorithms. Optimizations exist but add complexity. Most applications tolerate this scaling because k rarely exceeds small values like 5-10 participants.

Polynomials over finite fields are not generally injective (one-to-one mapping). The security property that matters: k distinct points uniquely determine a polynomial of degree less than k. This mathematical fact enables secret reconstruction while guaranteeing that insufficient shares reveal nothing.

Practical Applications

Cryptocurrency wallet security uses threshold schemes to distribute private key control among multiple devices or people. No single device compromise or person disappearance can eliminate access, but any threshold number can reconstruct keys for transactions.

Enterprise key management protects root certificates, encryption keys, and authentication credentials through organizational policies requiring multiple authorized personnel for access. This prevents both insider threats and single points of failure while maintaining audit trails.

Multi-party computation integrates secret sharing for privacy-preserving analysis across organizational boundaries. Participants can jointly compute results over their combined datasets without revealing individual contributions.

Cloud storage integration protects encryption keys through geographic distribution of shares. Cloud providers cannot access protected data, but authorized users can reconstruct keys through threshold mechanisms even if some storage locations become unavailable.

Operational Security Considerations

Share distribution requires secure channels to prevent interception during initial deployment. Share holders need secure storage protecting against physical compromise, social engineering, and technical attacks. Share reconstruction demands secure environments preventing observation of the reconstruction process or intermediate values.

Participant reliability affects practical security. Dead participants, forgotten passwords, or lost hardware can permanently prevent secret reconstruction if too many shares become unavailable. Higher thresholds increase security against compromise but reduce operational reliability.

Network-based reconstruction exposes reconstruction attempts to traffic analysis and timing correlation attacks. Local reconstruction in controlled environments provides superior operational security but may not be practical for distributed applications.

The mathematical elegance of information-theoretic security doesn't eliminate implementation vulnerabilities. Side-channel attacks, memory forensics, and social engineering remain viable attack vectors against deployed systems regardless of the underlying mathematical guarantees.